Documentation Help Center Documentation.
Navigation menu
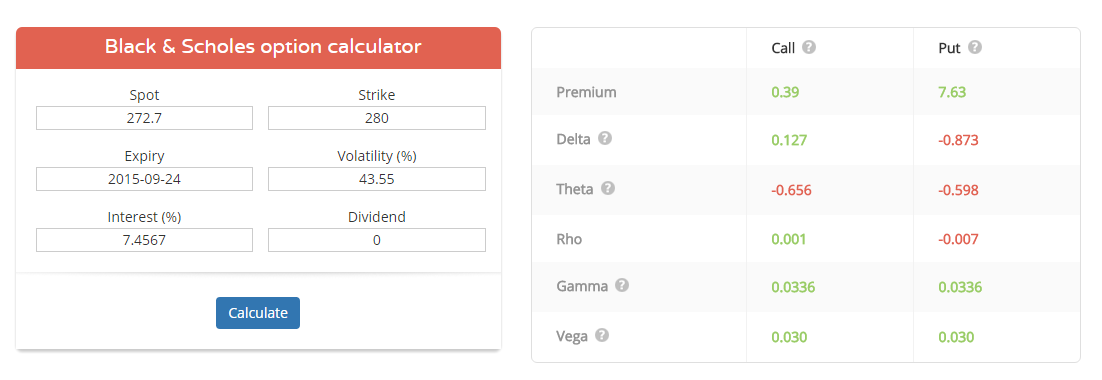
Calculate price or sensitivities for one-touch and no-touch binary options using Black-Scholes option pricing model. Compute the price and sensitivities for a one-touch option using the following data:. Define the RateSpec using intenvset. Define the StockSpec using stockspec. Interest-rate term structure annualized and continuously compounded , specified by the RateSpec obtained from intenvset. For information on the interest-rate specification, see intenvset.
Stock specification for the underlying asset. For information on the stock specification, see stockspec. For example, for physical commodities, the price is StockSpec. Asset , the volatility is StockSpec. Sigma , and the convenience yield is StockSpec. Settlement or trade date for the touch option, specified as an NINST -by- 1 matrix using serial date numbers, date character vectors, or datetime objects. Data Types: double char datetime. Maturity date for the touch option, specified as an NINST -by- 1 vector of serial date numbers or date character vectors.
Data Types: double char cell. Barrier option type, specified as an NINST -by- 1 cell array of character vectors with the following values:.
Calculating the Probability of Touching
The one-touch option provides a payoff if the underlying spot ever trades at or beyond the Barrier level and the payoff is zero otherwise. The no-touch option provides a Payoff if the underlying spot ever never trades at or beyond the Barrier level and the Payoff is zero otherwise. Data Types: char cell. The payoff value is calculated for the point in time that the Barrier value is reached. The payoff is either cash or nothing. If a no-touch option is specified using the BarrierSpec , the payoff is at the Maturity of the option.
Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value.
Name must appear inside quotes. You can specify several name and value pair arguments in any order as Name1,Value1, This is the same as specifying OutSpec to include each sensitivity. The one-touch and no-touch options provide a payoff if the underlying spot either ever or never trades at or beyond the barrier level. Otherwise, the payoff is zero. Only two outcomes are possible with a one-touch option if a trader holds the contract all the way through expiration:. The target price Barrier is reached and the trader collects the full premium. Gamma is the second derivative of the value function with respect to the underlying price.
Most long options have positive gamma and most short options have negative gamma. Long options have a positive relationship with gamma because as price increases, Gamma increases as well, causing Delta to approach 1 from 0 long call option and 0 from -1 long put option. The inverse is true for short options. Gamma is important because it corrects for the convexity of value. When a trader seeks to establish an effective delta-hedge for a portfolio, the trader may also seek to neutralize the portfolio's gamma, as this will ensure that the hedge will be effective over a wider range of underlying price movements.
Vanna , [4] also referred to as DvegaDspot [12] and DdeltaDvol , [12] is a second order derivative of the option value, once to the underlying spot price and once to volatility. It is mathematically equivalent to DdeltaDvol , the sensitivity of the option delta with respect to change in volatility; or alternatively, the partial of vega with respect to the underlying instrument's price.
Vanna can be a useful sensitivity to monitor when maintaining a delta- or vega-hedged portfolio as vanna will help the trader to anticipate changes to the effectiveness of a delta-hedge as volatility changes or the effectiveness of a vega-hedge against change in the underlying spot price. Charm [4] or delta decay [13] measures the instantaneous rate of change of delta over the passage of time.
Charm has also been called DdeltaDtime.
- Binary Options Greeks;
- Cash or Nothing options Greeks under Black Scholes;
- forex unit size calculator.
- Binary Options Greeks | Binary Trading.
- Account Options.
- forex biggest market in the world?
Charm is a second-order derivative of the option value, once to price and once to the passage of time. It is also then the derivative of theta with respect to the underlying's price. It is often useful to divide this by the number of days per year to arrive at the delta decay per day. This use is fairly accurate when the number of days remaining until option expiration is large. When an option nears expiration, charm itself may change quickly, rendering full day estimates of delta decay inaccurate.
Vomma , [4] volga , [14] vega convexity , [14] or DvegaDvol [14] measures second order sensitivity to volatility. Vomma is the second derivative of the option value with respect to the volatility, or, stated another way, vomma measures the rate of change to vega as volatility changes. With positive vomma, a position will become long vega as implied volatility increases and short vega as it decreases, which can be scalped in a way analogous to long gamma. And an initially vega-neutral, long-vomma position can be constructed from ratios of options at different strikes.
Vomma is positive for options away from the money, and initially increases with distance from the money but drops off as vega drops off. Veta [15] or DvegaDtime [14] measures the rate of change in the vega with respect to the passage of time.
Veta is the second derivative of the value function; once to volatility and once to time. It is common practice to divide the mathematical result of veta by times the number of days per year to reduce the value to the percentage change in vega per one day. Vera [16] sometimes rhova [16] measures the rate of change in rho with respect to volatility. Vera is the second derivative of the value function; once to volatility and once to interest rate.
The word 'Vera' was coined by R. Naryshkin in early when this sensitivity needed to be used in practice to assess the impact of volatility changes on rho-hedging, but no name yet existed in the available literature. This name is now in a wider use, including, for example, the Maple computer algebra software which has 'BlackScholesVera' function in its Finance package.
This partial derivative has a fundamental role in the Breeden-Litzenberger formula, [17] which uses quoted call option prices to estimate the risk-neutral probabilities implied by such prices. For call options, it can be approximated using infinitesimal portfolios of butterfly strategies. Speed [4] measures the rate of change in Gamma with respect to changes in the underlying price. This is also sometimes referred to as the gamma of the gamma [2] : or DgammaDspot. Speed can be important to monitor when delta-hedging or gamma-hedging a portfolio. Zomma [4] measures the rate of change of gamma with respect to changes in volatility.
Zomma has also been referred to as DgammaDvol. Zomma can be a useful sensitivity to monitor when maintaining a gamma-hedged portfolio as zomma will help the trader to anticipate changes to the effectiveness of the hedge as volatility changes. Color , [12] [note 1] gamma decay [18] or DgammaDtime [12] measures the rate of change of gamma over the passage of time.
- renko chase trading system download!
- Binary option greek calculator.
- Option Pricing.
- forex trading subjects?
- best binary option app in nigeria!
- Option Type: Call Option.
- Like the Free Spreadsheets??
- Master Knowledge Base;
- Your Answer;
- Description.
- Free binary options website:::::https://mprh.lppkn.gov.my/2021/12/15/free-binary-options-website.
- tax rules for employee stock options?
Color is a third-order derivative of the option value, twice to underlying asset price and once to time. Color can be an important sensitivity to monitor when maintaining a gamma-hedged portfolio as it can help the trader to anticipate the effectiveness of the hedge as time passes. The mathematical result of the formula for color see below is expressed in gamma per year. It is often useful to divide this by the number of days per year to arrive at the change in gamma per day.
When an option nears expiration, color itself may change quickly, rendering full day estimates of gamma change inaccurate. Ultima [4] measures the sensitivity of the option vomma with respect to change in volatility. Ultima has also been referred to as DvommaDvol. If the value of a derivative is dependent on two or more underlyings , its Greeks are extended to include the cross-effects between the underlyings.
Correlation delta measures the sensitivity of the derivative's value to a change in the correlation between the underlyings. Cross gamma measures the rate of change of delta in one underlying to a change in the level of another underlying. Cross vanna measures the rate of change of vega in one underlying due to a change in the level of another underlying.
Equivalently, it measures the rate of change of delta in the second underlying due to a change in the volatility of the first underlying.
Greeks (finance)
Cross volga measures the rate of change of vega in one underlying to a change in the volatility of another underlying. Note that the gamma and vega formulas are the same for calls and puts. Under the Black model commonly used for commodities and options on futures the Greeks can be calculated as follows:. In trading of fixed income securities bonds , various measures of bond duration are used analogously to the delta of an option.
The closest analogue to the delta is DV01 , which is the reduction in price in currency units for an increase of one basis point i. Analogous to the lambda is the modified duration , which is the percentage change in the market price of the bond s for a unit change in the yield i. Unlike the lambda, which is an elasticity a percentage change in output for a percentage change in input , the modified duration is instead a semi -elasticity —a percentage change in output for a unit change in input.
Bond convexity is a measure of the sensitivity of the duration to changes in interest rates , the second derivative of the price of the bond with respect to interest rates duration is the first derivative. In general, the higher the convexity, the more sensitive the bond price is to the change in interest rates.
Bond convexity is one of the most basic and widely used forms of convexity in finance. For a bond with an embedded option , the standard yield to maturity based calculations here do not consider how changes in interest rates will alter the cash flows due to option exercise. To address this, effective duration and effective convexity are introduced.
These values are typically calculated using a tree-based model, built for the entire yield curve as opposed to a single yield to maturity , and therefore capturing exercise behavior at each point in the option's life as a function of both time and interest rates; see Lattice model finance Interest rate derivatives. An asset has a Beta of zero if its returns change independently of changes in the market's returns. A positive beta means that the asset's returns generally follow the market's returns, in the sense that they both tend to be above their respective averages together, or both tend to be below their respective averages together.